시간 복잡도의 개념과 정렬 알고리즘(버블, 선택, 삽입, 퀵, 병합 정렬)을 간단하게 정리해보았다.

알고리즘 복잡도

알고리즘 복잡도 계산 항목은 다음과 같다. 공간 복잡도는 별도 게시물에서 다룰 예정이며, 시간 복잡도에 대해서 먼저 알아보고자 한다.

1. 시간 복잡도: 알고리즘 실행 속도
2. 공간 복잡도: 알고리즘이 사용하는 메모리 사이즈

Big O (빅-오) 표기법

알고리즘 성능 표기법 중 하나로, 알고리즘 최악의 실행 시간을 표기한다.

• 최악의 상황에서도 성능을 보장한다는 의미로 사용된다.
• 입력의 크기가 크면 클 수록 반복문이 알고리즘 수행 시간을 지배하기 때문에, n의 단위로 표기한다.
• 크기에 따라 기하급수적으로 시간 복잡도가 늘어날 수 있다.

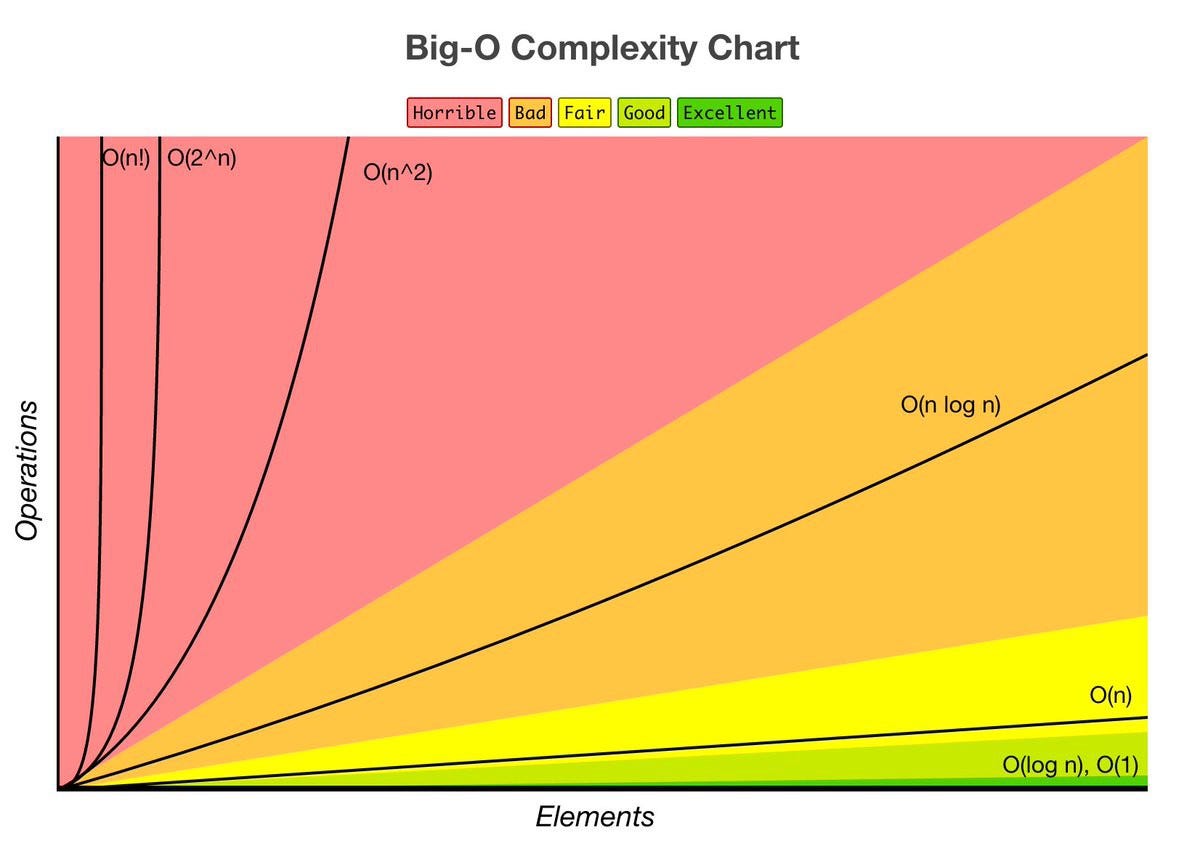
O(1) < O(𝑙𝑜𝑔𝑛) < O(n) < O(n𝑙𝑜𝑔𝑛) < O(𝑛^2) < O(2^n) < O(n!)

• 참고: log n 의 베이스는 2 - 𝑙𝑜𝑔2𝑛

기본 정렬

정렬은 데이터가 주어졌을 때 정해진 순서로 이를 나열하는 것이다. 정렬에는 여러 알고리즘이 있는데, 먼저 가장 쉽지만 성능은 낮을 수 있는 기본 정렬부터 알아보자.

1. 반복문이 두 개
2. 최악의 경우에는 O(n^2)
3. 완전 정렬이 되어 있는 상태라면 최선의 경우에는 O(n)

1. 버블정렬

첫 번째 인덱스부터 인접한 요소들을 비교하면서, 작은 요소를 앞에 놓는 스와핑을 반복하다보면 맨 뒤에는 가장 큰 수가 오게 되어있다.

• 한 번 턴을 돌고나면 값이 가장 높은 것이 무조건 맨 뒤로 가게 된다.
• 맨 뒤부터 비교할 값이 하나씩 줄어들게 된다.
• 한 턴에서 한 번도 스왑이 없을 경우에는 다음 턴이 필요 없다는 것을 알게 된다.

2. 선택 정렬

턴 마다 주어진 데이터 중 최소값을 선택한 다음, 최소값과 맨 앞의 값을 바꾸다 보면 가장 작은 값이 맨 앞에 오게 되어있다.

• 한 번 턴을 돌고나면 값이 가장 작은 것이 무조건 앞에 가게 된다.
• 맨 앞부터 비교할 값이 하나씩 줄어들게 된다.
• 한 턴에서 한 번도 스왑이 없을 경우에는 다음 턴이 필요 없다는 것을 알게 된다.

3. 삽입 정렬

두 번째 데이터부터 시작해 앞의 데이터들과 차례로 비교하면서 맞는 순서에 삽입한다.

• 첫 번째 기준점은 index = 1이고, 기준점이 하나씩 증가하게 된다.
• 앞의 요소들과 비교하면서 기준점의 요소보다 작으면 계속 바꿔준다.

고급 정렬

재귀 용법을 사용해서 리스트를 잘게 자른 다음, 잘린 리스트를 합치면서 다시 정렬하는 방법이다.

1. 퀵정렬

Pivot(기준점)을 정하고, 기준보다 작은 데이터는 왼쪽, 큰 데이터는 오른 쪽으로 모으는 작업을 반복한다.

• 보통 첫 번째 인덱스를 피봇으로 정한다.
• 피봇을 기준으로 만들어진 데이터들도 피봇을 기준을 또 정렬한다.
• 아래 예시에서 보듯 첫 번째 턴에서는 첫 번째 인덱스를 기준으로 쪼개게 된다.
• 이후 left 리스트를 나눌 수 있을 때까지 나누고 -> [pivot]과 합치고 -> right list를 나눈 값을 합치면 정렬된 결과가 완성된다.

def qsort(data):
    if len(data) <= 1:
        return data
    pivot = data[0]

    left = [ item for item in data[1:] if pivot > item ]
    right = [ item for item in data[1:] if pivot <= item ]

    return qsort(left) + [pivot] + qsort(right)

# first turn
[35, 43, 34, 51, 76, 70, 6, 75, 10, 55]
pivot = 35
left = [34, 6, 10]
right = [43, 51, 76, 70, 75, 55]

2. 병합 정렬

리스트 값이 하나가 될때까 split한 다음, 맨 앞 인덱스에서 순서대로 두 개씩 비교하면서 작은 값을 앞에 두면서 병합한다.

• 가운데 값을 기준으로 각 요소의 길이가 1이 될 때까지 split 한다
• 왼쪽부터 첫 번째 인덱스를 비교하면서 순서를 정렬한다.

def merge(left, right):
    merged = list()
    left_point, right_point = 0, 0

    # case1 - left/right 둘다 있을때
    while len(left) > left_point and len(right) > right_point:
        if left[left_point] > right[right_point]:
            merged.append(right[right_point]) # 왼쪽 값이 클 경우 오른쪽 값을 먼저 정렬
            right_point += 1
        else:
            merged.append(left[left_point])
            left_point += 1

    # case2 - left 데이터가 없을 때
    while len(left) > left_point:
        merged.append(left[left_point])
        left_point += 1

    # case3 - right 데이터가 없을 때
    while len(right) > right_point:
        merged.append(right[right_point])
        right_point += 1

    return merged


def mergesplit(data):
    if len(data) <= 1:
        return data
    medium = int(len(data) / 2)
    left = mergesplit(data[:medium]) # 왼쪽부터 길이가 1일 될떄까지 쪼개고, 두 값을 비교하면서 합치게 된다.
    right = mergesplit(data[medium:])
    return merge(left, right)

[89, 44, 18, 96, 68, 21, 26, 10, 65, 78]

# first turn of left
left: [89]
right: [44]
left: [44, 89] # 44와 89를 비교

# second turn of left
left: [18]
left: [96]
right: [68]
right: [68, 96] # 96과 68을 비교

# third turn of left
right: [18, 68, 96] # 18과 [96, 68]을 비교

# fourth turn of left
left: [18, 44, 68, 89, 96] # [44, 89]와 [18, 68, 96]을 비교

재귀용법을 사용하는 함수다보니 이해하는데 조금 시간이 걸렸다. 재귀 용법만 게시물로 따로 정리를 해야겠다.